Ciąg Fibonacciego
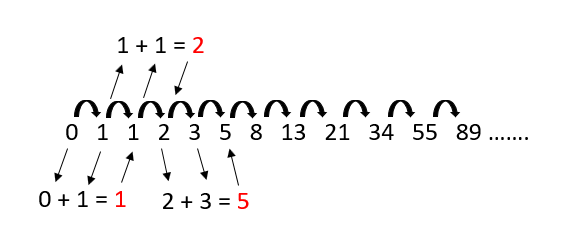
Za wszystkie głupstwa królów płacą ich narody
Horacy
Dla wielu ludzi matematyka skończyła się wraz z uzyskaniem świadectwa szkoły średniej. Za wszelką cenę nie chcą mieć z nią nic wspólnego, a na myśl o liczeniu przechodzą ich dreszcze. Na nic zdają się słowa powtarzane w dzieciństwie, iż matematyka jest królową nauk, ponieważ jest wszędzie. Lecz czy wystarczająco pokazano nam przykładów argumentując słowo "wszędzie"?
Doskonałym przykładem zastosowania matematyki w życiu jest tajemniczy ciąg Fibonacciego. Nie bez przypadku zostało użyte słowo tajemniczy, ponieważ pomimo badania go od tysięcy lat, wciąż nikomu nie udało się dowieźć skąd tak naprawdę się wziął.
Ciąg Fibonacciego to ciąg liczb w których każda następna to suma dwóch poprzednich. Przyjmując, że dwie pierwsze liczby są równe jeden, możemy zapisać go w ten sposób:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
Pierwszą właściwością jaką spełnia ciąg to powtarzająca się liczna 1,618 która powstaje wskutek podzielenia dwóch liczb obok siebie stojących. Na przykład 21/13 = 1,618. Czym większe liczby będziemy dzielić tym większe przybliżenie otrzymamy. Liczbę tę nazywa się "złotą liczbą" i oznacza grecką literą Fi.
Poza tym z liczb zawartych w ciągu Fibonacciego możemy utworzyć tak zwaną złotą spiralę.
Rysujemy kwadrat o długości boku równej pierwszej liczbie, czyli 1. Następnie również 1, następnie 2 i tak dalej. Zauważamy, że kwadraty i wpisana w nie spirala układa się w charakterystyczny sposób jak na rysunku poniżej.
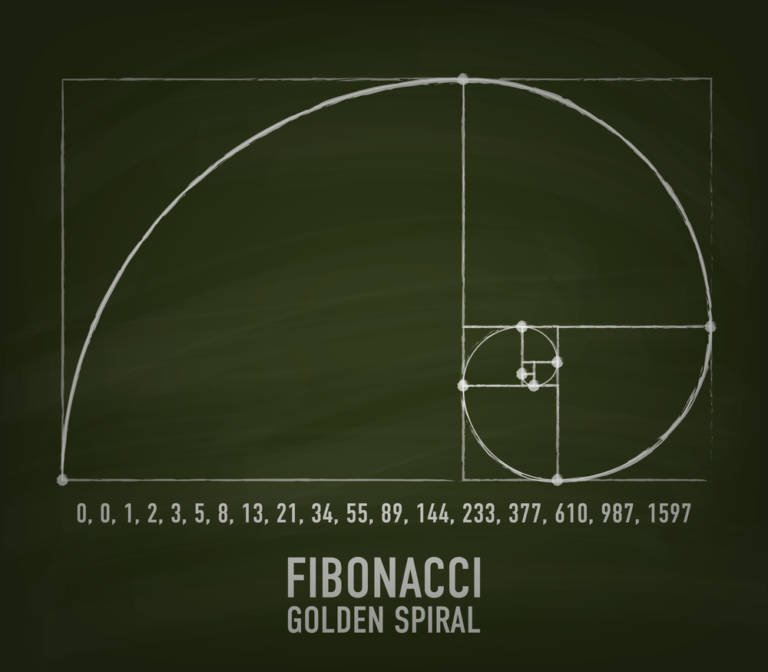 Żródło: depositphotos.com
Żródło: depositphotos.com
Wiedząc już na czym polega ciąg Fibonacciego zobaczmy, gdzie możemy go znaleźć.
W większości przypadków, zdrowo rozwinięta roślina będzie miała liczbę płatków odpowiadającą jednej z liczb z ciągu (np. 1 płatek – lilia calla, 2 – wiloczmlecz, 3 – irys, 5 – dzika róża, 8 – ostróżka, 13 – nagietek, 21 – stokrotki, 34 – złocień).
Dlatego tak ciężko znaleźć czterolistną koniczynę.
Złotą spiralę odnajdziemy w ogromnej ilości roślin i owoców:
 Żródło: depositphotos.com
Żródło: depositphotos.com
 Żródło: depositphotos.com
Żródło: depositphotos.com
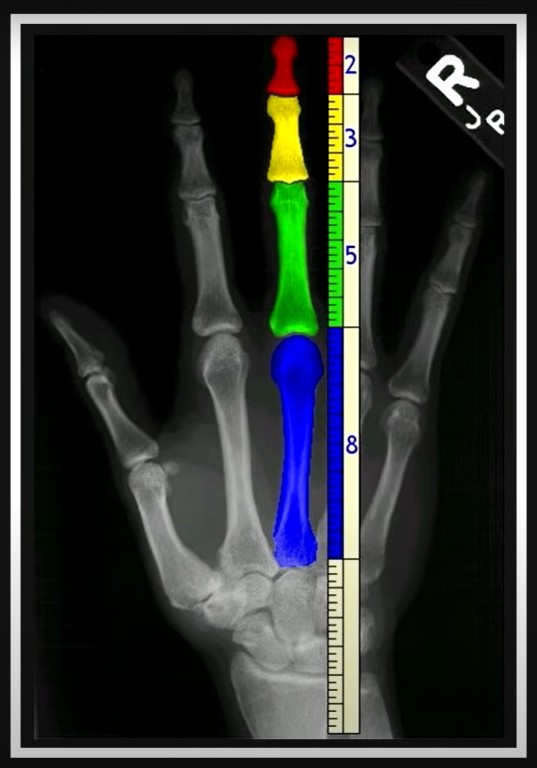
Znajdziemy ją również w innych dziedzinach życia, których przykłady zamieszczone są poniżej.





Źródła:
https://www.tajemnice-swiata.pl/ciag-fibonacciego/
https://www.youtube.com/watch?v=wb7kPaM8cfg